分数の足し算 文字式 246513-分数の足し算 文字式

文字式の分数を掛け算するには 3分でわかる計算 問題 割り算との関係

文字式の足し算引き算ができるのは 文字の部分が全く同じ項 (同類項) どうしのときだけである。 同類項の係数どうしを足し算、引き算する。 axbx = (ab)x (1)計算せよ。 x 2 3 2 3 x−4 2x 2 3x 5x 2 −4x 5x−7− (4x−3) (2)左の式から右の式を引いた差を求めよ。 7a12, 8a−6 (1) x 2 と 2 3 xが同類項である。 x 2 の係数は 1 2 、 2 3 x の係数は 2 3 、また定数項 (数字だけの項)は定数項どうしで計足し算 分数の足し算は、通分によって分母をそろえてから分子を足す ことで計算できます。 計算の手順は次の 3 ステップになります。 分数の足し算のやり方 通分（分母をそろえる） 分子同士を足す 約分する 例えば、次のように足し算を計算できます。 1 2 1 3 = 3 6 2 6 = 3 2 6 = 5 6 1 2 1 3 = 3 6 2 6 = 3 2 6 = 5 6 このページでは、 分母が同じ分数の足し算のやり方 と 分母が違う分数の足

分数の足し算 文字式

分数の足し算 文字式-この操作のことを「\(\dfrac{1}{4×5}\) を部分分数分解する」と言います。 微分や積分など、複雑な計算をするときは部分分数分解で「分数の足し算」に変形すると計算が楽になるケースが少なくありません。 部分分数分解をマスターすると、そういった複雑な計算でつまずく事がグッと少な文字式の分数の計算は 「小学校4年生からの分数」 これがわかってないと太刀打ちできません。 数学が苦手な中学生は 是非小学校からの分数の復習から 初めて欲しいと思います。 ちゃっかり宣伝ですけど 小学校4年生から6年生までの 分数の計算を

分数の文字式の足し算 引き算の計算方法

文字を使った式での商の表し方（負の数） 基本正負の数の除法の後半で見た通り、数字同士の割り算の場合、 $1\div 2$ や $1\div (2)$ は、 $\dfrac{1}{2}$ というように、分数の前にマイナスの記号を出します。$\dfrac{1}{2}$ や $\dfrac{1}{2}$ のままにはしません。分母が同じ分数式の足し算と引き算 分数の足し算や引き算をするとき、分母が同じであれば、分子を足したり引いたりするだけでしたね。\ \frac{3}{5}\frac{1}{5}=\frac{4}{5} \などと計算していました。 分数式の足し算や引き算の場合も同様です。分母の違う分数をたすには、分母を同じ数にしないと計算できません 。 そこで "分母の数どうしをかける" ことからとりかかります。 v字の部分が、チョウのしっぽ（胴体の先端）になります。 ②ななめにちょうの羽根をかき、分子のほうに触角をかく。

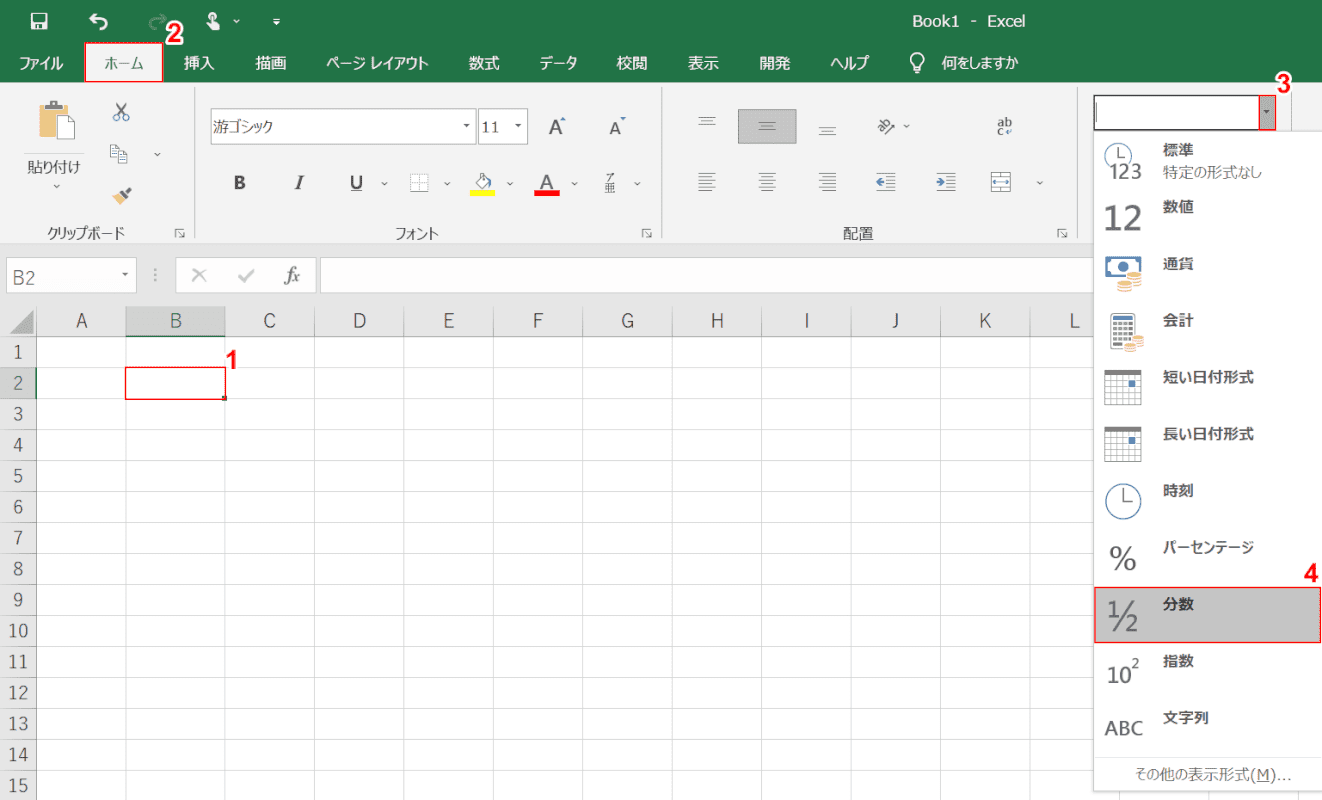
分数の足し算・引き算の手順 通分する（分母を揃える） 分子同士を計算する なぜ通分しなければいけないのか？ たとえば分母が等しい時を考えてみると、計算は普通の足し算・引き算と同じ要領でスムーズにできるのがわかります。 分母が同じという最低限覚えること 整数と分数の引き算は、整数を分数に直してから計算します。 1 − 1 3 ※引く分数が 1 3 なら 1 = 3 3 、 1 5 なら 1 = 5 5 のように整数を分数に直す = 3 3 − 1 3 = 3 − 1 3 2 3 整数と分数の足し算もやってみましょう。 整数と分数の引き算と分数を文字 列として入力 ①計算式を入力したい任意のセル（例：b2 エクセルで分数の計算する場合は、上記の「分数で足し算や掛け算などの

分数の足し算 文字式のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	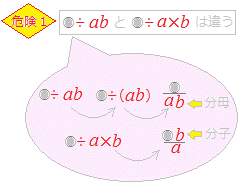約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
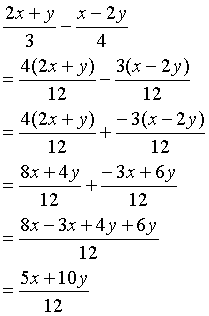約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	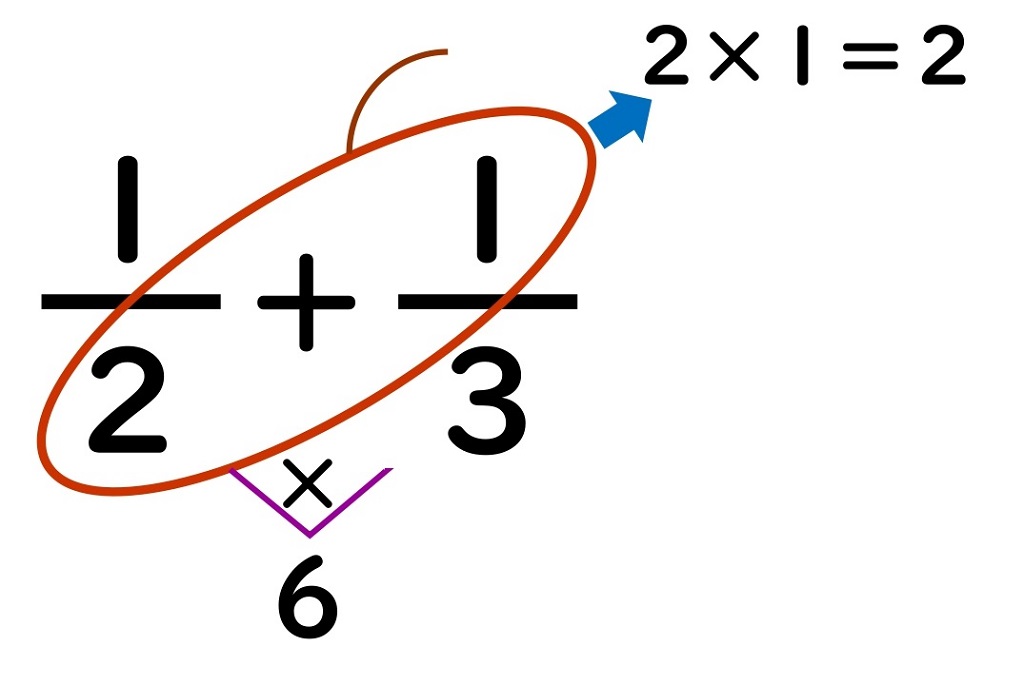約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	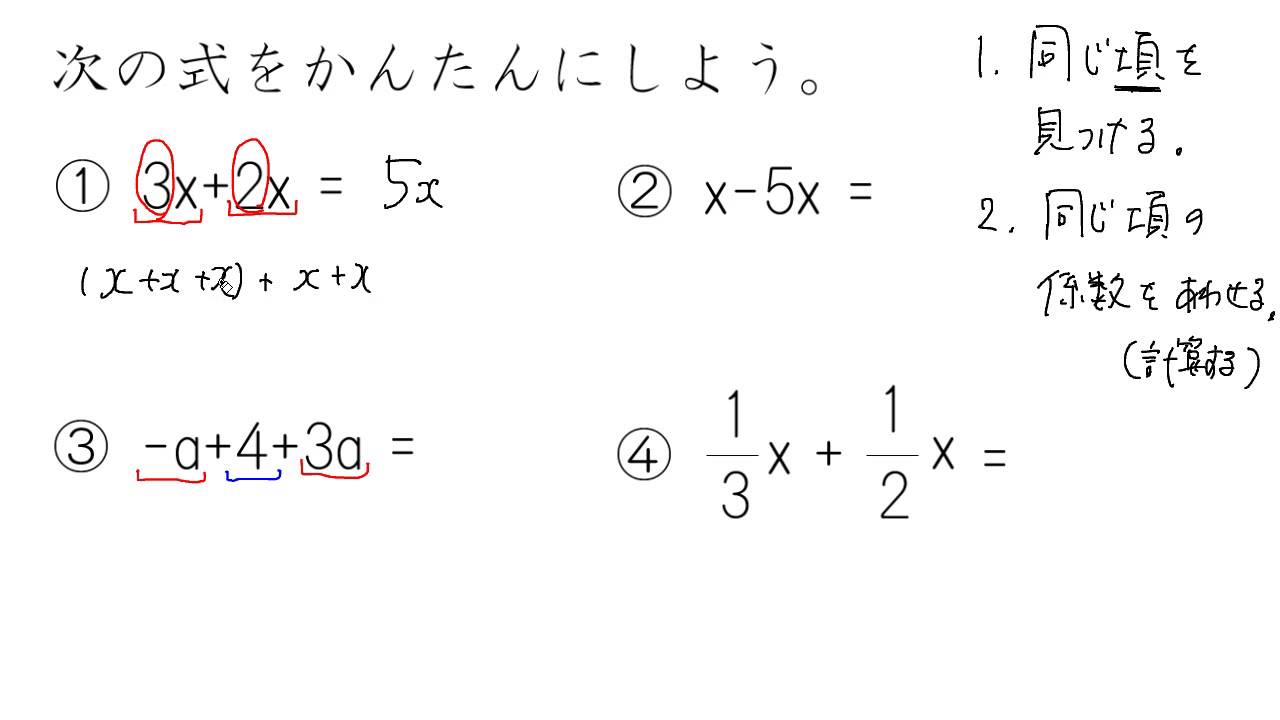約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	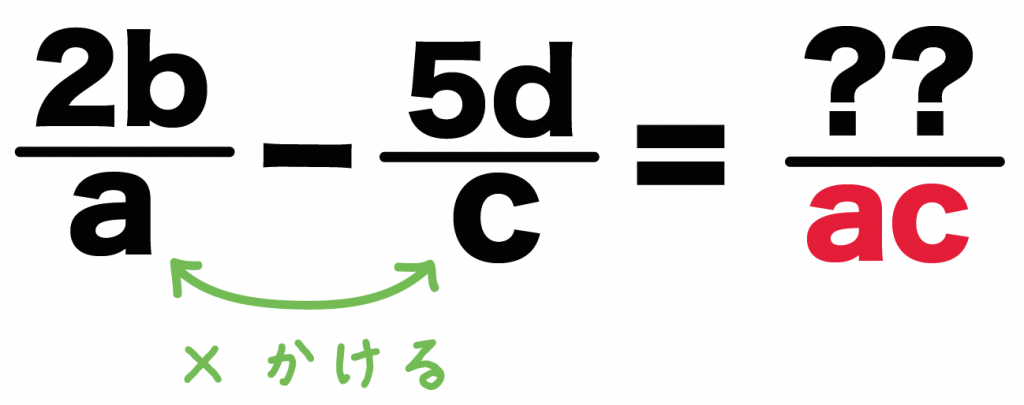約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	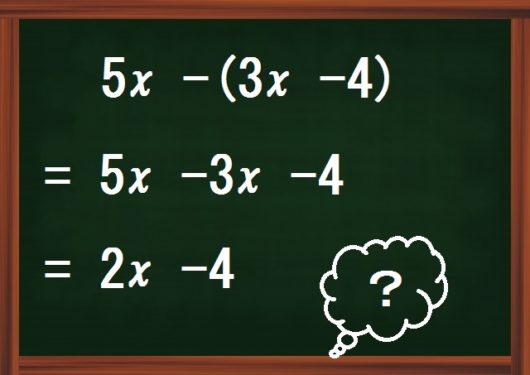約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	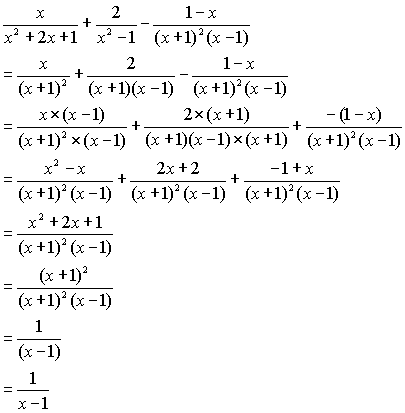約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
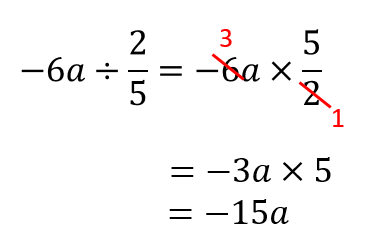約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
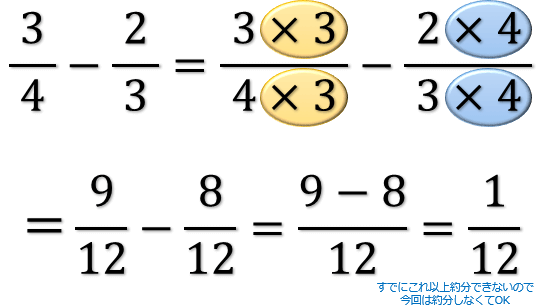約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	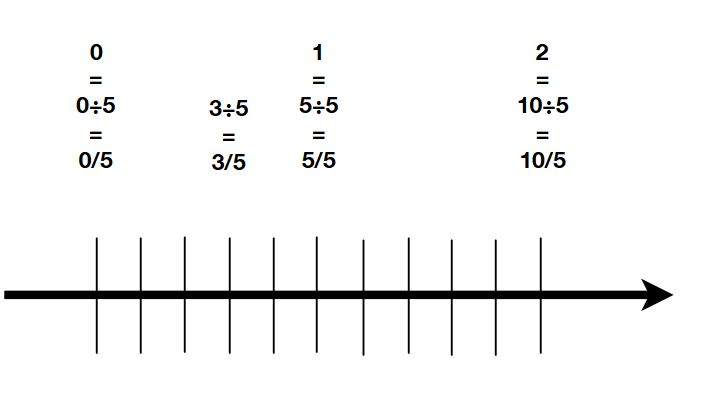約分を小学生並みにマスターさせる
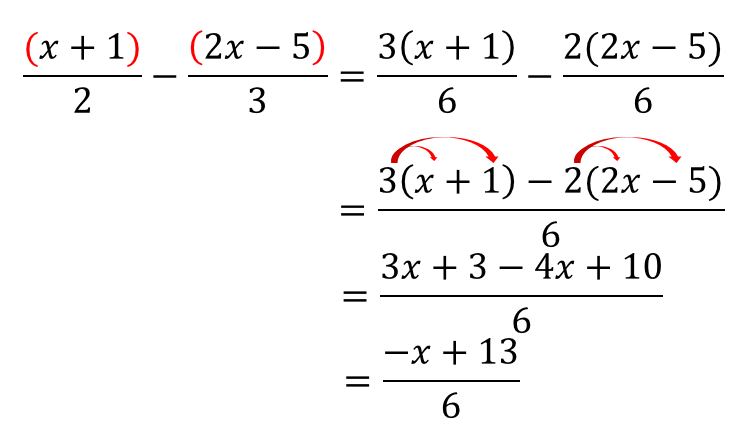約分を小学生並みにマスターさせる	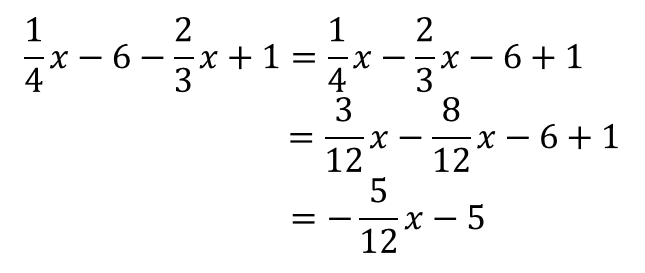約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
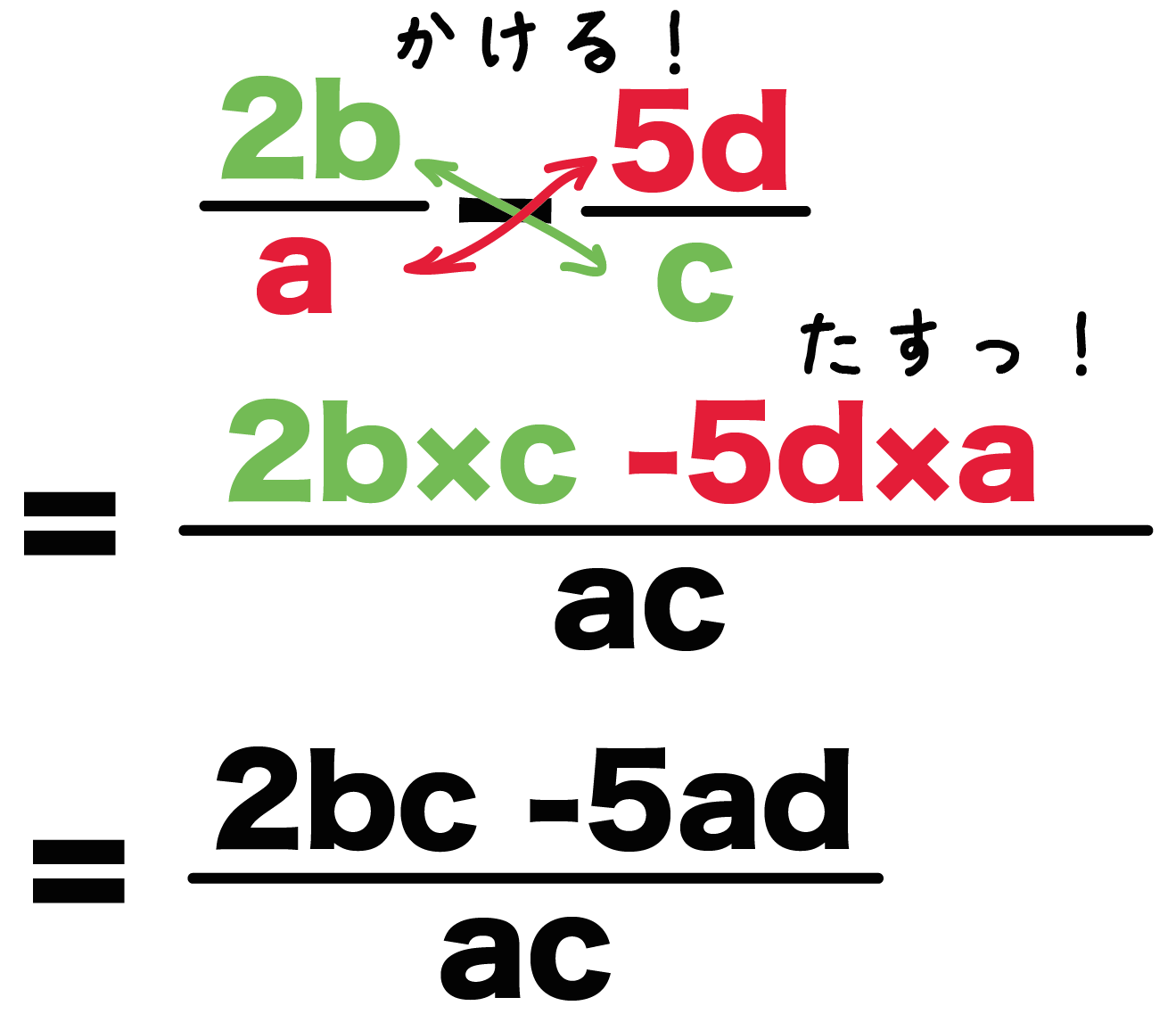約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる	約分を小学生並みにマスターさせる
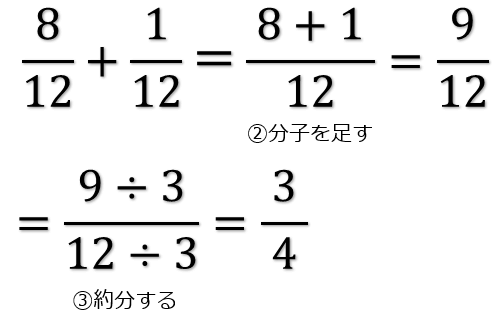約分を小学生並みにマスターさせる	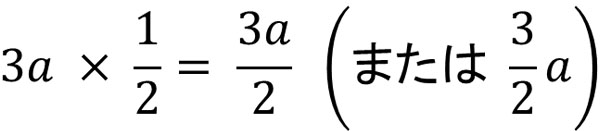約分を小学生並みにマスターさせる

もくじ 1 式の展開：分配法則でかっこを外せる 11 分配法則が成り立つ理由は面積で考える;文字の前につける数が1の場合には、1を省略して表します。 ただし $$11\times a=11a$$ $$01\times a=01a$$ このように、1という数字を含んでいたとしても11や01などは省略しないので気を付けてください。

Incoming Term: 分数の足し算 文字式,